Pairing for Cryptography

Bilinear Setting

Let $ \mathbb{G}_1,\mathbb{G}_2$ and $ \mathbb{G}_T$ be cyclic groups of prime order $ r$ Let $ g_1$ be a generator of $ \mathbb{G}_1$ and $ g_2$ be a generator of $ \mathbb{G}_2$. A bilinear pairing or bilinear map is an efficiently computable function $ e : \mathbb{G}_1 \times \mathbb{G}_2 \leftarrow \mathbb{G}_T$ such that:

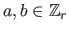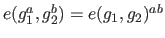
  1. Bilinearity: for all $ a,b\in\mathbb{Z}_r$ (the ring of integers modulo r) it holds that $ e(g_1^a,g_2^b) = e(g_1,g_2)^{ab}$

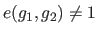
  2. Non-degeneracy: $ e(g_1,g_2)\ne 1$

The tuple $ (r,g_1,g_2,\mathbb{G}_1,\mathbb{G}_2,\mathbb{G}_T)$ is called asymmetric bilinear setting. On the other hand, if $ \mathbb{G}_1=\mathbb{G}_2=\mathbb{G}$ and g is a generator of $ \mathbb{G}$ then the tuple $ (r,g,\mathbb{G},\mathbb{G}_T)$ is called symmetric bilinear setting. In the symmetric setting the order of $ \mathbb{G}$ and $ \mathbb{G}_T$ need not to be prime.

The cryptographic relevance of a bilinear mapping stems from the fact that in cyclic groups that admit such a mapping the Decisional Diffie-Hellman assumption does not hold. Indeed, given $ (g,g^x,g^y,g^z)$ it is possible to check if $ z=xy$ (and thus solve the Decisional DH problem) by testing $ e(g,g^z)$ and $ e(g^x,g^y)$ for equality.

Multilinear Setting

An $ \ell$-group system consists of $ \ell$ cyclic groups $ \mathbb{G}_1,\ldots,\mathbb{G}_\ell$ of prime order $ r$, along with bilinear maps $ e_{i,j} : \mathbb{G}_i \times \mathbb{G}_j \rightarrow \mathbb{G}_{i+j}$ for all $ i,j\geq 1$ with $ i+j\leq\ell$. Let $ g_i$ be a canonical generator of $ \mathbb{G}_i$, the map $ e_{i,j}(g_i^a,g_j^b)=g_{i+j}^{ab}$. Finally, it can also be useful to define the group $ \mathbb{G}_0=\mathbb{Z}_{r}$ of exponents to which this pairing naturally extends.

The tuple $ \{r,\{\mathbb{G}_i,g_i\}_{i\in[\ell]}, \{e_{i,j}\}_{i,j\geq 1, i+j\leq\ell}\}$ is called multilinear setting.

Initializing Pairings

The Pairing interface provides access to the algebraic structures underlying the pairing computation and the pairing function.

The easiest way to obtain an instance of the Pairing interface is by using the factory provided by JPBC. The factory takes in input the pairing parameters and instantiates the appropriate classes. To generate the pairing parameters look at this page.

Let's now see how to use the factory.

Assume that the pairing parameters (for bilinear or multilinear maps) are stored in a file called params.properties. Then, the following code instantiate the appropriate class implementing the Pairing interface. 

import it.unisa.dia.gas.jpbc.*;
import it.unisa.dia.gas.plaf.jpbc.pairing.PairingFactory;

Pairing pairing = PairingFactory.getPairing("params.properties");

For bilinear maps only, to use the PBC wrapper and gain in performance, the usePBCWhenPossible property of the pairing factory must be set. 

PairingFactory.getInstance().setUsePBCWhenPossible(true);

Notice that, to effectively use the wrapper the usePBCWhenPossible property must be set before invoking the getPairing method.

Moreover, if PBC and the JPBC wrapper are not installed properly then the factory will resort to the JPBC pairing implementation.
The instructions to properly setup the PBC wrapper are here.

Accessing Algebraic Structures

The Pairing interface provides methods to access the algebraic structures involved in the pairing computation. Here are the methods: 

/* Return Zr */
Field Zr = pairing.getZr();

/* Return G1 */
Field G1 = pairing.getG1();

/* Return G2 */
Field G2 = pairing.getG2();

/* Return GT */
Field GT = pairing.getGT();

These algebraic structures can be also accessed by index with the following mapping. 

/* Return Zr */
Field Zr = pairing.getFieldAt(0);

/* Return G1 */
Field G1 = pairing.getFieldAt(1);

/* Return G2 */
Field G2 = pairing.getFieldAt(2);

/* Return GT */
Field GT = pairing.getFieldAt(3);

This is especially useful when dealing with multilinear maps to access the algebraic structures at different levels.
The number of algebraic structures available is given by the degree of the pairing that can be obtained by invoking the following method. 

int degree = pairing.getDegree();

In particular, there are degree+1 algebraic structures available indexed from 0 to degree.

Finally, elements of these algebraic structures can be initialized and manipulated for cryptographic operations as shown here.

Applying pairings

The Pairing interface provides methods to apply the pairing function. Given two elements Element in1, in2, belonging to the appropriate algebraic structures, their pairing can be computed by invoking the pairing method on input in1 and in2 as follows: 

Element out = pairing.pairing(in1, in2);

Furthermore, the Pairing interface let us compute the product of pairings. Given two vectors of the same length Element[] in1, in2 of elements belonging to the appropriate algebraic structures, their product pairing can be computed by invoking the pairing method on input in1 and in2 as follows: 

Element out = pairing.pairing(in1, in2);

Preprocessing

If it is known in advance that a particular value will be paired several times then time can be saved in the long run by using preprocessing. 

/* Get ready to perform a pairing whose first input is in1,
store the results of time-saving precomputation in ppp. */

Element in1 = pairing.getG1().newRandomElement();
PairingPreProcessing ppp = pairing.pairing(in1);

/* Compute the pairing using in2 and the preprocessed information
stored in ppp. The inputs to the pairing are the element
previously used to initialize ppp and the element in2. */

Element in2 = pairing.getG2().newRandomElement();
Element out = ppp.pairing(in2);

The result of the precomputation can be stored to be used later. The following code convert ppp to a byte array: 

byte[] pppBytes = ppp.toBytes();

To convert the byte array to an instance of the PairingPreProcessing interface use the following code: 

PairingPreProcessing ppp = pairing.getPairingPreProcessingFromBytes(pppBytes);